

Now we will solve the quadratic equation by factorization. By comparing this with ax 2 + bx + c = 0, we get a = 2. Example to Convert Standard to Intercept FormĬonsider the quadratic equation in standard form 2x 2 - 7x + 5 = 0. Thus, we just use any one of the solving quadratic equation techniques to find p and q. Here, (p, 0) and (q, 0) are the x-intercepts of the quadratic function f(x) = ax 2 + bx + c) and hence p and q are the roots of the quadratic equation. Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - p)(x - q) = 0. Let us consider the above example 2 (x - 1) 2 + 1 = 0 and let us convert it back into standard form.Ģx 2 - 4x + 3 = 0 -> Standard FormĬonverting Standard Form of Quadratic Equation into Intercept Form The process of converting the vertex form of a quadratic equation into the standard form is pretty simple and it is done by simply evaluating (x - h) 2 = (x - h) (x - h) and simplifying. Substituting a = 2, h = 1, and k = 1 in the vertex form a (x - h) 2 + k = 0, we get:Ģ (x - 1) 2 + 1 = 0 Converting Vertex Form to Standard Form To convert it into the vertex form, let us find the values of h and k. Comparing this with ax 2 + bx + c = 0, we get a = 2, b = -4, and c = 3. Example of Converting Standard Form to Vertex FormĬonsider the quadratic equation 2x 2 - 4x + 3 = 0. Thus, we can use the formulas h = -b/2a and k = (4ac - b 2) / (4a) to convert the standard to vertex form. Let us just set them equal to know the relation between the variables.Īx 2 + bx + c = ax 2 - 2ah x + (ah 2 + k)Ĭomparing the coefficients of x on both sides, Note that the value of 'a' is the same in both equations.
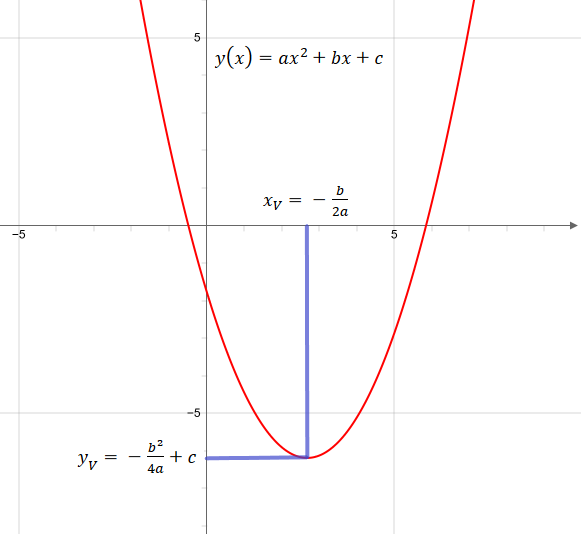
Let us convert the standard form of a quadratic equation ax 2 + bx + c = 0 into the vertex form a (x - h) 2 + k = 0 (where (h, k) is the vertex of the quadratic function f(x) = a (x - h) 2 + k). Converting Standard Form of Quadratic Equation into Vertex Form


 0 kommentar(er)
0 kommentar(er)
